Beregn Areal af Trekant: En Simpel Guide til Geometri

Beregn areal af trekant – en guide til at finde en af de grundlæggende egenskaber af en trekant

En trekant er en grundfigur af geometri og matematik. En trekant består af tre sider og tre vinkler. En af de grundlæggende egenskaber af en trekant er areal. Areal af en trekant er området af det flade geometriske figur af en trekant. I matematik og geometri, arkitektur, ingeniørarbejde eller endda dagligt liv, kan beregning af areal af trekant være nyttig for mange formål. I denne artikel vil vi guide dig gennem trinene til beregning af areal af en trekant og svare på nogle almindelige spørgsmål i FAQ-sektionen.

Trin til beregning af areal af trekant

For at beregne arealet af en trekant skal du kende længden af grundlinjen og højden. Her er nogle trin, du kan følge for at finde arealet af en trekant.

1. Mål længden af grundlinjen

Det første skridt er at finde længden af grundlinjen. Grundlinjen er den side af trekanten, som ligger på den flade overflade. Mål længden af grundlinjen fra startpunkt til slutpunkt.

2. Mål højden af trekanten

Højden er den lodrette afstand fra grundlinjen til det punkt, hvor trekanten mødes. Mål afstanden fra startpunktet af grundlinjen til det modsatte punkt af trekanten. Hvis du ikke har adgang til den lodrette afstand, kan du bruge theoremet i Pythagoras til at beregne højden af ​​trekanten.

3. Beregn arealet af trekanten

Når du har målt længden af ​​grundlinjen og højden af ​​trekanten til grundlinjen, kan du beregne arealet af trekanten ved at bruge formlen ‘areal = 1/2 × grundlinje × højde’. Sæt værdierne for grundlinjen og højden i denne formel, og du vil få det samlede areal af trekanten.

Eksempel: Beregn areal af trekant

For at forstå beregning af areal af trekanten, kan du tage et eksempel. Lad os sige, at længden af ​​grundlinjen er 10 cm og højden af trekanten på grundlinjen er 8 cm. Så vi skal finde ud af arealet af trekanten.

Arealfomlen er A = 1/2 × b × h. Sætter vi værdierne på plads, får vi:

A = 1/2 × 10 cm × 8 cm

= 40 kvadratcentimeter.

Så arealet af trekanten er 40 kvadratcentimeter.

FAQ:

1. Hvordan kan jeg måle højden af ​​trekanten, hvis den ikke er vinkelret?

Hvis du ikke kan måle lodret afstand mellem grundlinjen og toppunktet af trekanten, kan du bruge theoremet i Pythagoras. Theoremet i Pythagoras siger, at i en retvinklet trekant er kvadratet på hypotenuse (den længste side) lig med summen af ​​kvadraterne på de to andre sider.

Så højden af trekanten kan findes ved hjælp af teoremet i Pythagoras. Formlen er:

Højde² = Hypotenuse² – Halv-grundlinje²

Sæt værdierne i denne formel og få højden af trekanten.

2. Hvordan kan jeg finde længden af ​​grundlinjen, hvis den ikke er lige?

Hvis du ikke kan finde længden af ​​grundlinjen, fordi den ikke er lige, kan du beregne længden af ​​grundlinjen ved hjælp af trigonometri. Hvis du kender to vinkler og en sidelængde, kan du beregne sidelængderne og vinklen mellem dem ved hjælp af trigonometriske relationer såsom sinus, cosinus og tangent.

3. Hvad er forskellen mellem en højde og en sidelængde i en trekant?

En sidelængde er en af de tre linjer, der forbinder tre hjørner af trekanten. En højde er en lodret afstand fra en af trekantens sider til det toppunkt, der er vinkelret på denne side af trekanten. Højdens længde kan afhænge af trekantens vinkel, mens sidelængderne er konstante.

4. Hvorfor er areal af trekanten vigtigt?

Areal af trekanten er en af ​​de grundlæggende egenskaber af en trekant, og det er vigtigt i mange situationer. Areal af trekanten er nyttigt i matematik og geometri, arkitektur, ingeniørarbejde, måling af græsplæner og mange andre formål. Areal af trekanten anvendes også i ligninger af cirkler og ellipser, og i trigonometri i beregning af afstande og vinkler.

Konklusion

Arealet af en trekant er en af de grundlæggende egenskaber af en trekant. Det er vigtigt i mange situationer i matematik og geometri, arkitektur, ingeniørarbejde og mange andre formål. Beregning af areal af trekant er ikke svært. Hvis du kender grundlinjen og højden af ​​trekanten, kan du nemt finde arealet ved hjælp af formlen ‘areal = 1/2 × grundlinje × højde’. Selv hvis du ikke kan finde højden af ​​trekanten, kan du bruge theoremet i Pythagoras til at beregne den.

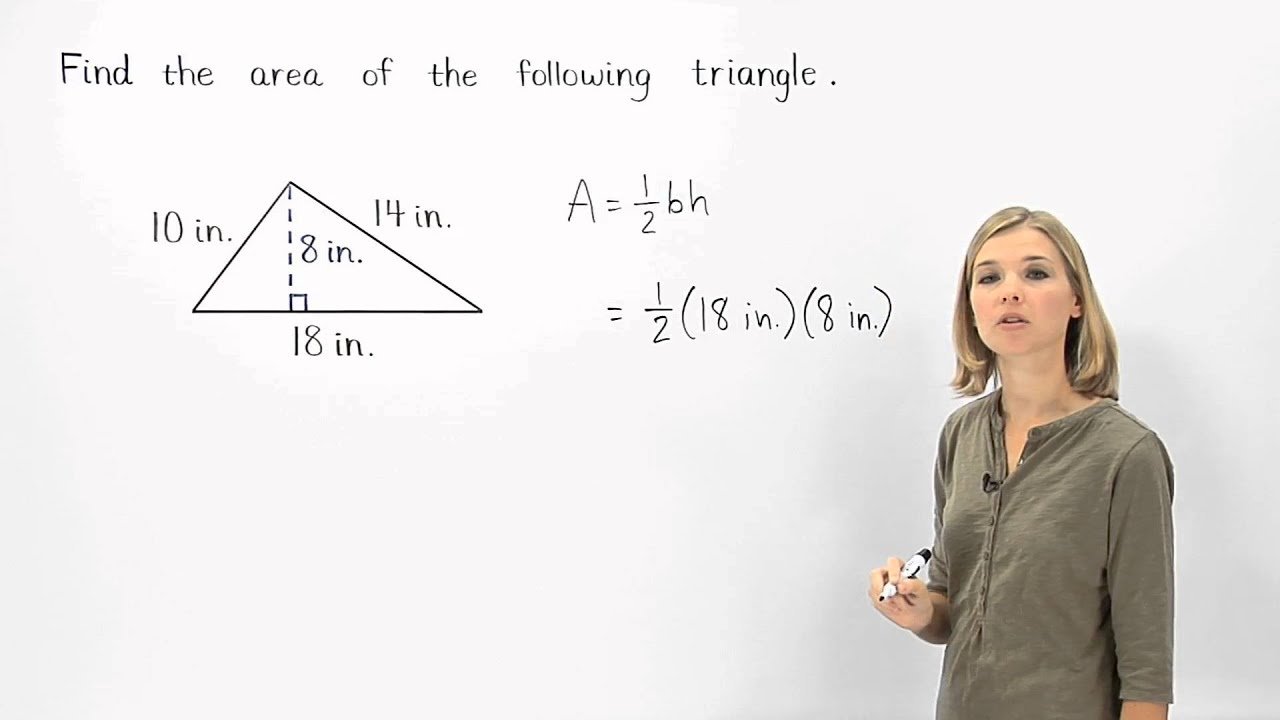
Areal af vilkårlig trekant

En trekant er en figur, der består af tre linjestykker og tre hjørner, hvor hvert hjørne er forbundet af et linjestykke. Areal af en trekant er den mængde plads, som figuren optager i planen. Arealen af en trekant afhænger af længden af de tre linjestykker.

For at beregne areal af en vilkårlig trekant er det nødvendigt at kende to størrelser: længden af basen og højden af trekanten.

Længden af basen er en af de tre linjestykker, der definerer trekanten. Basen kan være enten den korteste eller den længste linjestykke i trekanten. Højden af trekanten er afstanden mellem basen og det tredje punkt, som ikke er forbundet til basen. Højden vil normalt danne en ret vinkel med basen.

For en retvinklet trekant, hvor en af hjørnerne er en ret vinkel, kan arealet beregnes ved at multiplicere længden af basen med højden af trekanten og derefter dividere med 2.

Areal af en vilkårlig trekant kan beregnes ved anvendelse af formel af Heron. Formlen af Heron er en formel, der giver arealet af en trekant ud fra længden af de tre sider.

Formel af Heron:

s = (a+b+c)/2

Areal = √[s(s-a)(s-b)(s-c)]

Hvor s = halvperimeter, a = længden af den ene sidestykke, b = længden af den anden sidestykke og c = længden af den tredje sidestykke.

Hvad er en vilkårlig trekant?

En vilkårlig trekant er en trekant, hvor alle tre sider ikke nødvendigvis er lige lange, og ingen tre hjørner er lige store. En vilkårlig trekant kan være enhver form, så længe den har de tre linjestykker, der sammen definerer både sider og hjørner.

Hvordan måler man højden af en trekant?

Højden af en trekant er afstanden mellem basen og det tredje punkt, som ikke er forbundet til basen. Hvis der er en ret vinkel i trekanten, er højden defineret som den linje, der danner en ret vinkel til basen. For at måle højden af en trekant skal man trække en lige linje fra det tredje punkt, som ikke er forbundet til basen, ned til basen for at lave en ret vinkel.

Hvordan beregner man arealet af en vilkårlig trekant uden at kende højden?

Det er ikke muligt at beregne arealet af en trekant uden at kende højden. Højden er en nødvendig parameter for at kunne beregne arealet af en trekant.

Hvad er forskellen på en ligebenet trekant og en ligesidet trekant?

En ligebenet trekant er en trekant, hvor to af siderne er lige lange, og det tredje er kortere. Højden af trekanten vil være forskellig fra længden af de ens sider. En ligesidet trekant er en trekant, hvor alle tre sider har samme længde. I en ligesidet trekant vil højden af trekanten være lig med længden af en af siderne ganget med kvadratroden af 3 dividere med 2.

Hvad er forskellen på en retvinklet trekant og en skæv trekant?

En retvinklet trekant er en trekant, hvor en af hjørnerne er en ret vinkel, og de to andre hjørner ikke er lige. En skæv trekant er enhver trekant, der ikke er en retvinklet trekant.

Kan en trekant have en negativ højde?

Nej, en trekant kan ikke have en negativ højde. Højden af en trekant er en afstandsmængde og er dermed selv en positiv værdi.

Konklusion

Areal af en trekant er en vigtig geometrisk parameter, der er nødvendig for at løse mange forskellige problemer inden for matematik og fysik. Arealet af en vilkårlig trekant kan beregnes ved anvendelse af formel af Heron. Formlen af Heron er en formel, der giver arealet af en trekant ud fra længden af de tre sider. Længden af basen og højden af trekanten er nødvendige størrelser for at beregne arealet af en trekant. Højden af en trekant er defineret som afstanden mellem basen og det tredje punkt, som ikke er forbundet til basen. En vilkårlig trekant er en trekant, hvor alle tre sider ikke nødvendigvis er lige lange, og ingen tre hjørner er lige store. For en retvinklet trekant kan arealet beregnes ved at multiplicere længden af basen med højden af trekanten og derefter dividere med 2.

Ligebenet trekant areal – en introduktion

En trekant med to sider af samme længde kaldes en ligebenet trekant. Denne form for trekant har nogle særlige egenskaber, som kan være nyttige at kende, især når det kommer til at beregne dens areal. I denne artikel vil vi se nærmere på, hvad en ligebenet trekant er, hvordan man beregner dens areal, og hvilke andre faktorer der kan påvirke dette.

Hvad er en ligebenet trekant?

En trekant består af tre sider og tre vinkler. I en ligebenet trekant er to af siderne af samme længde, mens den tredje side kan have en anden længde. Derudover er de to vinkler, der vedhæfter de to lige sider, også af samme størrelse, mens den tredje vinkel kan have en anden størrelse. Dette giver trekanten et symmetrisk udseende, og det gør det også nemt at identificere en ligebenet trekant, når man ser den.

Ligebenet trekants egenskaber

En af de vigtigste egenskaber ved en ligebenet trekant er, at de to vinkler mellem de to lige sider er lige store. Dette betyder, at trekanten kan deles op i to retvinklede trekanter, hver med en af de lige sider som hypotenusen og halvdelen af den tredje side som den ene katete. Dette kan være nyttigt for at løse geometriske problemer, hvor man har brug for at finde længderne af sider eller vinkler.

En anden egenskab ved en ligebenet trekant er, at dens højde – linjen, der er trukket fra vinklen på modsatte side af den lige side ned til basen – deler basen i to lige store dele. Dette betyder, at arealet af trekanten også kan beregnes ved at gange halvdelen af basen med højden. Dette vil vi se nærmere på i næste afsnit.

Hvordan beregner man arealet af en ligebenet trekant?

Der er flere måder at beregne arealet af en trekant på, men hvis man har med en ligebenet trekant at gøre, er der en særlig formel, man kan bruge. Formlen tager udgangspunkt i trekantens base og højde, som begge er kendte værdier. Basen er den side, der er modsat den mindste vinkel, mens højden er linjen, der er trukket fra toppen af denne vinkel ned til basen.

Formlen er som følger:

Areal = (basen x højden) / 2

Lad os betragte et eksempel. Forestil dig en ligebenet trekant med en base på 6 cm og en højde på 4 cm. For at beregne arealet, skal vi sætte disse værdier ind i formlen:

Areal = (6 x 4) / 2 = 12 cm²

Så arealet af denne trekant er 12 kvadratcentimeter.

Ligebenet trekant areal FAQ

1. Kan man have en ligebenet trekant med tre forskellige sider?

Nej, det er ikke muligt. For at have to lige sider skal de to tilhørende vinkler også være ens, hvilket definerer en ligebenet trekant. Hvis alle tre sider er forskellige, kan vinklerne også have forskellige størrelser, men trekanten vil ikke være ligebenet.

2. Kan man beregne arealet af en trekant på andre måder end ved at bruge basen og højden?

Ja, der er flere formler, man kan bruge til at beregne arealet af en trekant, afhængigt af hvilke oplysninger der er til rådighed. Én sådan formel er Herons formel, der tager udgangspunkt i længderne af alle tre sider. En anden er ved at bruge sinus- eller cosinusrelationerne, hvis man kender vinklerne og siderne.

3. Kan man bruge Pythagoras’ sætning til at beregne længderne af en ligebenet trekant?

Ja, det kan man. Hvis man kender længden af den mindste side og højden til denne side, kan man bruge Pythagoras’ sætning til at finde længden af den tredje side. Dette kan være nyttigt, hvis man skal finde længden af en diagonal eller hypotenusen i en større figur.

4. Kan man bruge en ligebenet trekant til at finde positionen af en ting?

Ja, det kan man, hvis man har oplysninger om de andre vinkler og sider i trekanten. Hvis man kender to vinkler og en side i en trekant, kan man bruge trigonometri til at finde længden af de andre sider og dermed positionen af en ting i forhold til trekanten. Dette kan være nyttigt i fx landmåling eller navigering.