Beregning af retvinklede trekanter: En grundig guide

Beregning af retvinklede trekanter er en vigtig disciplin inden for matematik. En retvinklet trekant er en trekant, hvor én af vinklerne er 90 grader. I denne artikel vil vi kigge på forskellige måder, man kan beregne retvinklede trekanter på.

Formler for beregning af sider og vinkler i retvinklede trekanter

Hvis man kender to sidelængder eller sider og en vinkel i en retvinklet trekant, kan man finde de manglende sider og vinkler med hjælp af trigonometriske formler.

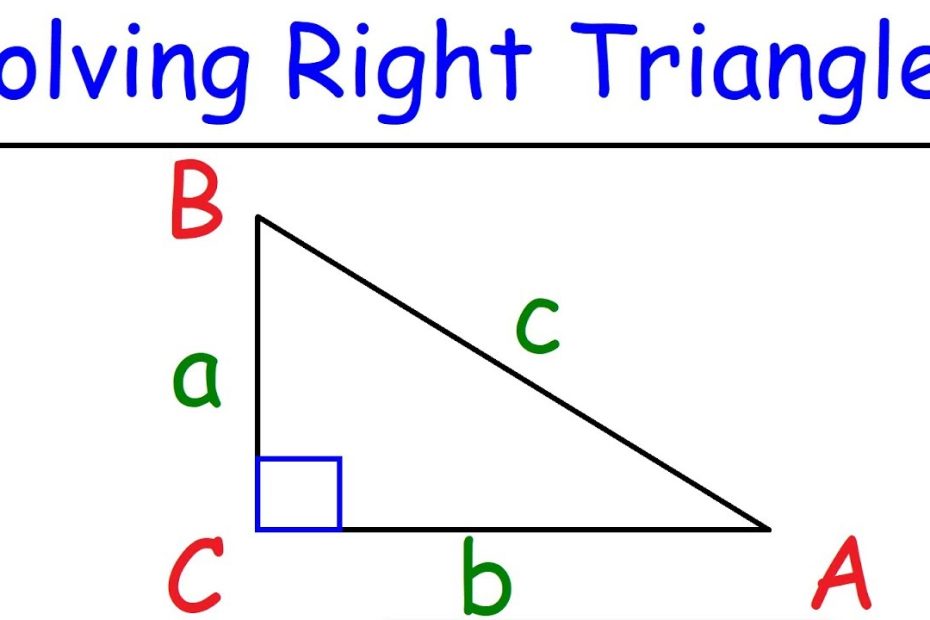
I en retvinklet trekant betegnes den længste side som hypotenusen, og de to andre sider kaldes kateter. Hvis vi betegner hypotenusen som c, og kateterne som a og b, så er der følgende formler, som kan bruges til at beregne sider og vinkler i en retvinklet trekant:

Pythagoras’ læresætning: a^2 + b^2 = c^2

Sinusrelationen: sin A = a/c, sin B = b/c, sin C = c/a

Cosinusrelationen: cos A = b/c, cos B = a/c, cos C = a/b

Tangensrelationen: tan A = a/b, tan B = b/a

Eksempel:

I en retvinklet trekant er hypotenusen 10 cm og det ene katet 6 cm. Hvad er længden af det andet katet, og hvad er størrelsen af den rette vinkel?

Vi kan finde længden af det andet katet ved at anvende Pythagoras’ læresætning:

6^2 + b^2 = 10^2

36 + b^2 = 100

b^2 = 64

b = 8

Så det andet katet er 8 cm.

Vi kan finde størrelsen af den rette vinkel ved at anvende sinusrelationen:

sin A = a/c = 6/10

A = sin^-1(6/10)

A ≈ 36,9 grader

Så den rette vinkel er omkring 36,9 grader.

Anvendelse af beregning af retvinklede trekanter

At kunne beregne sider og vinkler i retvinklede trekanter er vigtigt i mange sammenhænge, både inden for matematik og i forskellige praktiske situationer.

Inden for matematik kan beregning af retvinklede trekanter indgå i opgaver og problemstillinger inden for trigonometri, geometri og algebra. Det kan fx være relevant, når man skal bestemme afstanden mellem to punkter på en flade eller i rummet, beregne højder eller afstande til fjerne genstande, eller når man skal forudsige bevægelser i bølger eller vibrationer.

I praktiske situationer kan det også være nødvendigt at kunne beregne sider og vinkler i retvinklede trekanter. Det kan fx være relevant i byggeri, når man skal bestemme længder og vinkler på forskellige konstruktioner, eller i landmåling og geodesi, når man skal bestemme afstande og højder til faste punkter på jorden. Det kan også være relevant inden for navigation og sejlads, hvor man skal bestemme retninger og afstande til forskellige punkter på havet eller landjorden.

FAQs

Hvad er en retvinklet trekant?

En retvinklet trekant er en trekant, hvor én af vinklerne er 90 grader.

Hvad er Pythagoras’ læresætning?

Pythagoras’ læresætning siger, at i en retvinklet trekant er summen af kvadraterne på kateterne lig med kvadratet på hypotenusen. Matematisk kan det skrives som a^2 + b^2 = c^2, hvor a og b er kateterne, og c er hypotenusen.

Hvad er sinusrelationen?

Sinusrelationen bruges til at beregne en vinkels størrelse i en retvinklet trekant, når man kender forholdet mellem en sidelængde og hypotenusen. Sinusrelationen kan skrives som sin A = a/c, sin B = b/c, eller sin C = c/a, hvor a, b og c er siderne i trekanten, og A, B og C er de tilhørende vinkler.

Hvad er cosinusrelationen?

Cosinusrelationen bruges til at beregne en sides længde i en retvinklet trekant, når man kender størrelsen på vinklen mellem den og hypotenusen. Cosinusrelationen kan skrives som cos A = b/c, cos B = a/c, eller cos C = a/b, hvor a, b og c er siderne i trekanten, og A, B og C er de tilhørende vinkler.

Hvad er tangensrelationen?

Tangensrelationen bruges til at beregne forholdet mellem kateterne i en retvinklet trekant. Tangensrelationen kan skrives som tan A = a/b eller tan B = b/a, hvor a og b er kateterne, og A og B er de tilhørende vinkler.

Beregn vinkel i retvinklet trekant

En retvinklet trekant er en geometrisk form med tre vinkler, hvoraf en er en ret vinkel på 90 grader. For at beregne vinklerne i en retvinklet trekant, skal man benytte trigonometriske funktioner, såsom sinus, cosinus og tangens. Disse funktioner kan bruges til at finde de manglende vinkler og længder i en trekant, når man kender nogle af de andre vinkler og længder.

Trigonometriske funktioner i en retvinklet trekant

For at forstå, hvordan man beregner vinklerne i en retvinklet trekant, skal man først kende til de trigonometriske funktioner, der kan bruges. De mest almindelige trigonometriske funktioner i en retvinklet trekant er sinus, cosinus og tangens.

Sinus (sin) repræsenterer forholdet mellem længden af den modsatte side (modstående vinkel) og hypotenusen i trekanten:

sin(vinkel) = modstående side/hypotenusen

Cosinus (cos) repræsenterer forholdet mellem længden af den tilstødende side (vinkel ved siden af) og hypotenusen i trekanten:

cos(vinkel) = tilstødende side/hypotenusen

Tangens (tan) repræsenterer forholdet mellem længden af den modsatte side (modstående vinkel) og længden af den tilstødende side:

tan(vinkel) = modstående side/tilstødende side

Disse funktioner kan bruges til at finde de manglende vinkler eller længder i en retvinklet trekant, når man kender nogle af de andre vinkler eller længder.

Eksempel på beregning af en vinkel i en retvinklet trekant

Lad os tage et eksempel på, hvordan man kan beregne en vinkel i en retvinklet trekant. Vi har en trekant med en ret vinkel, en kendt længde af en side (tilstødende) og en ukendt vinkel (modstående).

Først kan vi benytte cosinus-funktionen til at finde længden af hypotenusen:

cos(vinkel) = tilstødende side/hypotenusen

hypotenusen = tilstødende side/cos(vinkel)

Nu kan vi tage anvende sinus-funktionen til at finde længden af den ukendte side:

sin(vinkel) = modstående side/hypotenusen

modstående side = hypotenusen x sin(vinkel)

Nu kan vi beregne den ukendte vinkel:

vinkel = arcsin(modstående side/hypotenusen)

I dette tilfælde vil vi kende en vinkel og længden af den hypotenus, hvilket betyder, at vi kan bruge tangent-funktionen i stedet for sinus og cosinus:

tan(vinkel) = modstående side/tilstødende side

modstående side = tilstødende side x tan(vinkel)

Nu kan vi finde længden af hypotenusen:

hypotenusen = modstående side/sin(vinkel)

Og derefter kan vi beregne den manglende vinkel:

vinkel = arctan(modstående side/tilstødende side)

FAQs

1. Hvad er en retvinklet trekant?

En retvinklet trekant er en geometrisk form med tre vinkler, hvoraf en er en ret vinkel på 90 grader.

2. Hvordan kan trigonometriske funktioner bruges til at beregne vinkler i en retvinklet trekant?

Trigonometriske funktioner, såsom sinus, cosinus og tangens, kan bruges til at finde de manglende vinkler og længder i en retvinklet trekant, når man kender nogle af de andre vinkler og længder.

3. Hvad er forskellen mellem sinus, cosinus og tangens?

Sinus repræsenterer forholdet mellem længden af den modsatte side (modstående vinkel) og hypotenusen i trekanten. Cosinus repræsenterer forholdet mellem længden af den tilstødende side (vinkel ved siden af) og hypotenusen i trekanten. Tangens repræsenterer forholdet mellem længden af den modsatte side (modstående vinkel) og længden af den tilstødende side.

4. Hvordan kan man beregne en vinkel i en retvinklet trekant, når man kender længden af en side og vinklen ved siden af?

Man kan benytte cosinus-funktionen til at finde længden af hypotenusen. Derefter kan man anvende sinus-funktionen til at finde længden af den ukendte side. Endelig kan man finde den manglende vinkel ved at tage arcsin af forholdet mellem den modstående side og hypotenusen.

5. Hvordan kan man beregne en vinkel i en retvinklet trekant, når man kender længden af en side og den modstående vinkel?

Man kan benytte tangent-funktionen til at finde længden af den modstående side. Derefter kan man finde længden af hypotenusen ved at tage forholdet af den modstående side og sinus af den modstående vinkel. Endelig kan man beregne den manglende vinkel ved at tage arctan af forholdet mellem den modstående side og den tilstødende side.

Beregn sidelængde i retvinklet trekant

En retvinklet trekant er en geometrisk figur med en vinkel på 90 grader. Det betyder, at to af trekantens sider står lodret på hinanden, mens den tredje side udgør hypotenusen, som er den længste side. Når man kender længden af to af trekantens sider, kan man beregne resten af trekanten, så som længden af den sidste side, vinklerne og arealet.

Her følger en grundig gennemgang af de metoder, som man kan anvende for at beregne sidelængderne i en retvinklet trekant.

Pythagoras’ læresætning

En af de mest kendte og brugte metoder er Pythagoras’ læresætning, som siger, at i en retvinklet trekant er summen af kvadraterne på kateterne (de to sider, som ikke er hypotenusen) lig med kvadratet på hypotenusen. Eller sagt med andre ord:

a^2 + b^2 = c^2

Her er a og b de to kateter i trekanten, mens c er hypotenusen.

Hvis man kender længden af to af trekantens sider, kan man altså beregne den tredje side. Lad os tage et eksempel:

Vi har en retvinklet trekant, hvor de to kateter er henholdsvis 3 cm og 4 cm lange. Hvad er længden af hypotenusen?

Vi ved, at a = 3 cm og b = 4 cm. Ved at sætte disse ind i Pythagoras’ læresætning får vi:

3^2 + 4^2 = c^2

9 + 16 = c^2

25 = c^2

Nu kan vi tage kvadratroden af begge sider og få:

5 = c

Så hypotenusen i trekanten er 5 cm lang.

Så denne metode er god, når man kender de to kateter, men ikke hypotenusen.

Sinus, cosinus, tangens

En anden metode til at beregne sidelængder i retvinklede trekanter er at bruge sinus, cosinus og tangens. Disse er forholdet mellem forskellige sider i en trekant, og de defineres som følger:

sinus = modstående katete / hypotenusen

cosinus = tilstødende katete / hypotenusen

tangens = modstående katete / tilstødende katete

Ved hjælp af disse forhold kan man beregne sidelængder og vinkler i trekanten. Lad os tage et eksempel:

Vi har en retvinklet trekant, hvor vinklen ved siden af hypotenusen er 30 grader, og hypotenusen er 10 cm lang. Hvad er længden på den ene katete?

Vi ved, at cosinus = tilstødende katete / hypotenusen. Da vinklen ved kateten er 30 grader, kan vi bruge cosinus på denne vinkel, og vi får:

cos 30 = tilstødende katete / 10

Da cos 30 er 0,866, kan vi isolere tilstødende katete og få:

tilstødende katete = 0,866 x 10

tilstødende katete = 8,66

Så den længde af den ene katete er 8,66 cm.

Arealet af en trekant

For at beregne arealet af en retvinklet trekant, skal man kende længden af to af siderne (kateterne eller hypotenusen). Arealet beregnes ved at gange en katete med den anden og derefter tage halvdelen af resultatet. Så formlen er:

areal = (a x b) / 2

Her er a og b de to sider, som danner trekantens grundlinje, mens halvdelen af produktet beregner trekantens areal.

Lad os tage et eksempel:

Vi har en retvinklet trekant, hvor de to kateter er henholdsvis 6 cm og 8 cm lange. Hvad er trekantens areal?

Arealet beregnes ved:

areal = (6 x 8) / 2

areal = 24

Så trekantens areal er 24 kvadratcentimeter.

FAQs:

Q: Hvordan kan man bruge Pythagoras’ læresætning til at beregne arealet af en trekant?

A: Pythagoras’ læresætning bruges til at beregne sidelængder i en trekant og kan ikke bruges til at beregne trekantens areal.

Q: Hvad sker der, hvis vinklen i en retvinklet trekant ikke er 90 grader?

A: En trekant med en vinkel på 90 grader er en retvinklet trekant, og hvis vinklen ikke er 90 grader, er det ikke en retvinklet trekant.

Q: Er der en formel til at beregne alle sider og vinkler i en retvinklet trekant?

A: Nej, der er ikke en enkelt formel til at beregne alle sider og vinkler i en retvinklet trekant. Forskellige metoder kan bruges afhængigt af de kendte oplysninger om trekanten.

Q: Hvordan kan man anvende sinus, cosinus og tangens til at beregne vinkler i en retvinklet trekant?

A: Sinus, cosinus og tangens kan bruges til at beregne vinkler i en retvinklet trekant, hvis man kender længden af to af trekantens sider. Ud fra disse kan man beregne en af vinklerne.