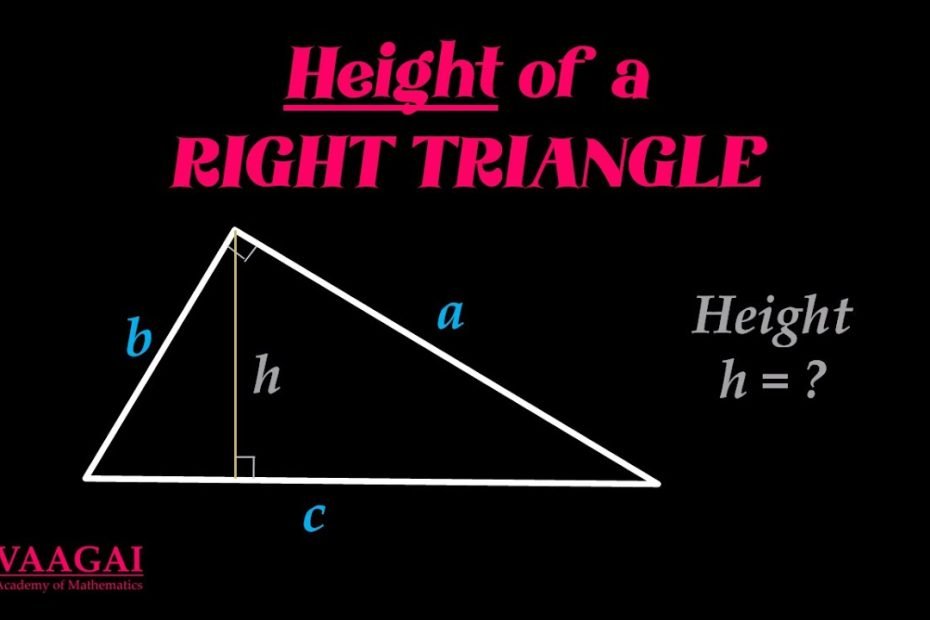
beregn højden i en retvinklet trekant
Trin-for-trin guide til at finde højden i en retvinklet trekant
Trin 1: Kend længden af de to kateter
For at beregne højden i en retvinklet trekant, skal du først kende længden af de to kateter. Kateterne er de to sider, der tilsammen danner den rette vinkel. Lad os kalde de to kateter for a og b.
Trin 2: Find arealet af trekanten ved at multiplicere længden af de to kateter og dividere med 2
Før vi kan finde højden, skal vi finde arealet af trekanten. Dette gøres ved at multiplicere længden af de to kateter og herefter dividere med 2. Formlen for at finde arealet af en trekant er A = (a * b) / 2.
Trin 3: Kend længden af hypotenusen
Nu hvor vi kender længden af de to kateter og arealet af trekanten, kan vi finde længden af hypotenusen. Hypotenusen er den tredje side i trekanten, der er modsat den rette vinkel. Lad os kalde længden af hypotenusen for c.
Vi kan finde længden af hypotenusen ved hjælp af Pythagoras’ sætning, der siger, at i en retvinklet trekant er summen af kvadraterne på kateterne lig med kvadratet på hypotenusen. Formelt skrevet, c^2 = a^2 + b^2.
Trin 4: Divider arealet af trekanten med længden af hypotenusen for at finde højden
Endelig kan vi finde højden af trekanten ved at dividere arealet af trekanten med længden af hypotenusen. Formlen for at finde højden af en retvinklet trekant er h = (2A) / c.
Sådan kan du beregne højden i en retvinklet trekant ved hjælp af disse fire trin.
Ofte stillede spørgsmål om at beregne højden i en retvinklet trekant
1. Hvordan kan jeg kende længden af hypotenusen i en retvinklet trekant?
Hypotenusen i en retvinklet trekant kan findes ved hjælp af Pythagoras’ sætning. Det kræver, at du kender længden af de to kateter, der danner den rette vinkel.
2. Kan jeg finde højden ved hjælp af en anden formel?
Ja, der er alternative måder at finde højden af en retvinklet trekant på. En anden formel er h = b * sin(alpha), hvor b er længden på en katet og alpha er vinklen mellem hypotenusen og kateten, du bruger til at finde højden.
3. Hvorfor er det vigtigt at kende højden i en retvinklet trekant?
At kende højden i en retvinklet trekant er vigtig, fordi det gør det muligt at finde arealet af trekanten. Arealet kan bruges til at beregne, hvor meget maling eller andet materiale der skal bruges til at dække trekanten, eller til at finde ud af dens volumen og masse.
4. Kan jeg finde højden, hvis jeg kun kender længden af en katet og vinklen mellem katet og hypotenusen?
Ja, du kan finde højden ved hjælp af formelen h = a * sin(alpha), hvor a er længden af kateten, og alpha er vinklen mellem hypotenusen og kateten, du bruger til at finde højden.
5. Kan jeg beregne højden ved hjælp af trigonometri?
Ja, du kan bruge trigonometri til at finde højden i en retvinklet trekant. Formlen er h = c * sin(beta), hvor c er længden af hypotenusen, og beta er vinklen mellem den ene katet og hypotenusen.
Konklusion
At beregne højden i en retvinklet trekant er en relativt simpel proces, som kan udføres ved at følge de fire trin, vi har gennemgået i denne artikel. Det kræver kendskab til længden af de to kateter og arealet af trekanten, og ved hjælp af Pythagoras’ sætning og en simpel division kan højden findes. Der er også alternative formler og metoder til at finde højden i en retvinklet trekant, og det er vigtigt at kende højden, da den kan bruges til at beregne arealet, volumen og masse af trekanten.
Søgeord søgt af brugere: beregn sidelængde i retvinklet trekant, stumpvinklet trekant, retvinklet trekant beregner, beregn sider i trekant, find katete i retvinklet trekant, beregn vinkel i retvinklet trekant, beregn vinkel i trekant, beregn hypotenusen i en retvinklet trekant
Se videoen om “beregn højden i en retvinklet trekant”
Height of a Right Triangle | In English
se mere: cungcaphangchinhhang.com
Billeder relateret til beregn højden i en retvinklet trekant
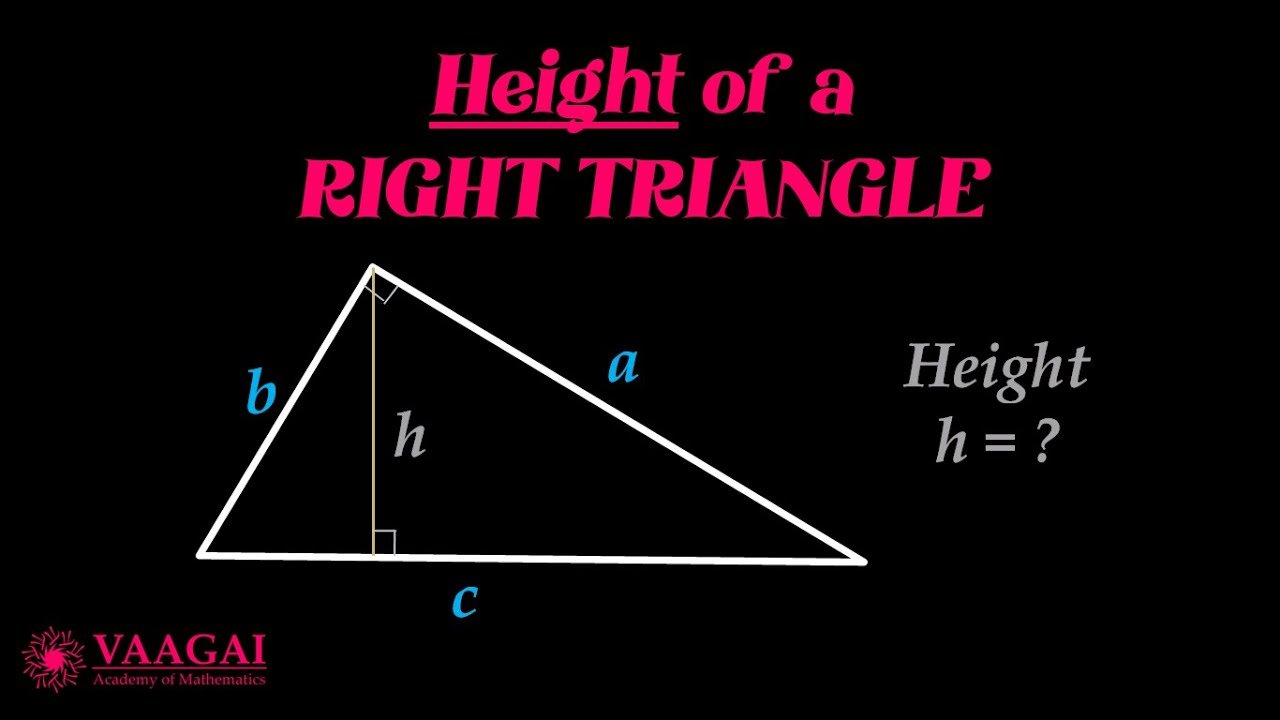
beregn sidelængde i retvinklet trekant
En retvinklet trekant er en trekant med en ret (90 graders) vinkel mellem to af sine sidelængder. Den tredje sidelængde, der er modsat den rette vinkel, kaldes hypotenusen. Ofte er det nødvendigt at beregne sidelængder i en retvinklet trekant, og her vil denne artikel være en hjælp.
Formler til beregning af sidelængder i en retvinklet trekant
Der er flere forskellige formler, der kan anvendes til beregning af sidelængder i en retvinklet trekant. De mest almindelige er:
– Pythagoras’ sætning
– sinus
– cosinus
– tangens
Pythagoras’ sætning
Pythagoras’ sætning er den mest kendte formel til beregning af sidelængder i en retvinklet trekant. Den siger, at summen af kvadraterne på de to kateter (de to andre sidelængder end hypotenusen) er lig med kvadratet på hypotenusen. Det kan udtrykkes således:
c^2 = a^2 + b^2
hvor c er hypotenusen, og a og b er kateter.
Eksempel:
Hvis a = 3 cm og b = 4 cm, så kan hypotenusen c findes ved at sætte disse værdier ind i Pythagoras’ sætning:
c^2 = 3^2 + 4^2
c^2 = 9 + 16
c^2 = 25
c = 5 cm
Sinus
Sinus er en trigonometrisk funktion, der kan bruges til beregning af sidelængder i en retvinklet trekant. Sinus af en vinkel er defineret som forholdet mellem vinkelens modstående katete og hypotenusen. Det kan udtrykkes således:
sin(A) = a/c
hvor a er den modstående katete, c er hypotenusen, og A er vinklen i modsætning til a.
Eksempel:
Hvis A = 30 grader og hypotenusen c = 6 cm, kan siden a beregnes ved at sætte disse værdier ind i sinusformlen:
sin(30) = a/6
a = 6*sin(30)
a = 3 cm
Cosinus
Cosinus er også en trigonometrisk funktion, der kan bruges til beregning af sidelængder i en retvinklet trekant. Cosinus af en vinkel er defineret som forholdet mellem vinkelens tilstødende katete og hypotenusen. Det kan udtrykkes således:
cos(A) = b/c
hvor b er den tilstødende katete, c er hypotenusen, og A er vinklen i modsætning til b.
Eksempel:
Hvis A = 60 grader og hypotenusen c = 8 cm, kan siden b beregnes ved at sætte disse værdier ind i cosinusformlen:
cos(60) = b/8
b = 8*cos(60)
b = 4 cm
Tangens
Tangens er den sidste trigonometriske funktion, der kan bruges til beregning af sidelængder i en retvinklet trekant. Tangens af en vinkel er defineret som forholdet mellem vinkelens modstående katete og tilstødende katete. Det kan udtrykkes således:
tan(A) = a/b
hvor a er den modstående katete, b er den tilstødende katete, og A er vinklen i modsætning til a.
Eksempel:
Hvis A = 45 grader og siden a = 4 cm, kan siden b beregnes ved at sætte disse værdier ind i tangensformlen:
tan(45) = 4/b
b = 4/tan(45)
b = 4 cm
Brug af disse formler gør det nemt at beregne sidelængder i en retvinklet trekant.
FAQs
1. Hvordan ved jeg, om en trekant er en retvinklet trekant?
En retvinklet trekant har en ret (90 graders) vinkel mellem to af sine sidelængder. For at finde ud af, om en trekant er retvinklet, skal du kontrollere, om den har en ret vinkel.
2. Hvilken side kaldes hypotenusen?
Den side, der ligger modsat den rette vinkel, kaldes hypotenusen.
3. Hvilken formel er den mest kendte til beregning af sidelængder i en retvinklet trekant?
Pythagoras’ sætning er den mest kendte og mest anvendte formel til beregning af sidelængder i en retvinklet trekant.
4. Kan jeg bruge sinus, cosinus og tangens til at beregne sidelængder i enhver trekant?
Nej, sinus, cosinus og tangens kan kun bruges til beregning af sidelængder i en retvinklet trekant.
5. Hvorfor er det vigtigt at vide, hvordan man beregner sidelængder i en retvinklet trekant?
At kunne beregne sidelængder i en retvinklet trekant er nyttigt i en lang række sammenhænge, herunder ingeniørarbejde, byggeprojekter og træning i matematik og fysik. Det er også nyttigt i dagligdagen til planlægning af udendørsprojekter, når du skal beregne længden af en teltstang, flagstang eller tagrende, der skal monteres på en væg, eller når du vil beregne højden af et træ eller en bygning.
stumpvinklet trekant
En stumpvinklet trekant er også kendt som en oblik trekant, som stammer fra det latinske ord “obliquus”, der betyder skrå. Dette refererer til den vinkel, som er skrå i forhold til de andre to. Dette betyder også, at den længste side, som er modsat den stumpvinklede vinkel, er den skrå side.
Hvordan beregner man en stumpvinklet trekant?
For at beregne en stumpvinklet trekant, skal man vide mindst én af følgende faktorer: længden af en af siderne, størrelsen af en af de indre vinkler eller højden til den længste side. Med disse oplysninger kan man bruge forskellige geometriske formler til at beregne andre faktorer i trekanten.
For eksempel, hvis man kender længden af den længste side, kan man bruge sinus, cosinus eller tangens til at finde størrelsen af en af de andre vinkler eller længden af en af de andre sider. Hvis man kender størrelsen af en indre vinkel, kan man bruge den generelle formel for vinkelsummen i en trekant (180 grader) til at finde størrelsen af de andre to vinkler.
En stumpvinklet trekant kan også løses ved at bruge Pythagoras’ sætning, som beskriver forholdet mellem længden af de tre sider i en retvinklet trekant. Ved at bruge Pythagoras’ sætning og trigonometriske formler kan man finde længden af de tre sider og størrelsen af de tre vinkler i en stumpvinklet trekant.
Hvornår bruger man en stumpvinklet trekant?
En stumpvinklet trekant bruges ofte i matematikundervisningen, da den giver eleverne mulighed for at undersøge og forstå geometriske formler og metoder. Denne type trekant kan også være nyttig i andre fag, såsom fysik og ingeniørfag, hvor den kan bruges til at beregne afstande, hastigheder og styrker.
Stumpvinklede trekanter kan også have praktiske anvendelser i hverdagen. For eksempel kan man bruge en stumpvinklet trekant til at beregne, hvor højt en bygning er, ved at måle afstanden fra bygningen og skråningen til toppen af bygningen.
Hvad er en rektangulær trekant?
En rektangulær trekant er en type trekant, hvor en af vinklerne er en ret vinkel, hvilket betyder, at den er på 90 grader. Dette betyder også, at den længste side, som kaldes hypotenusen, er vinkelret på den korteste side, som kaldes kateten. En rektangulær trekant er også kendt som en retvinklet trekant.
Rektangulære trekanter er vigtige i matematik og fysik, da de bruges til at beregne afstande, hastigheder og styrker. Pythagoras’ sætning, som beskriver forholdet mellem længden af de tre sider i en retvinklet trekant, er også en vigtig formel i matematik og fysik.
Hvad er forskellen mellem en stumpvinklet trekant og en spidsvinklet trekant?
En stumpvinklet trekant og en spidsvinklet trekant er to forskellige typer trekant, som adskiller sig i deres indre vinkler. En stumpvinklet trekant har en indre vinkel, der er mindre end 90 grader, mens en spidsvinklet trekant har tre indre vinkler, der alle er mindre end 90 grader.
En anden forskel mellem de to typer trekant er, at den længste side i en stumpvinklet trekant er modsat den stumpvinklede vinkel, mens den længste side i en spidsvinklet trekant er modsat den spidsvinklede vinkel.
Hvad er forskellen mellem en trekants median og en trekants højde?
En trekants median er en linje, der forbinder en vinkelspids med midtpunktet af den modsatte side i trekanten. En trekants højde er en linje, der er vinkelret på en af siderne i trekanten og går fra modsatte vinkel til den pågældende side til det punkt, hvor højden skærer den pågældende side.
Forskellen mellem de to linjer er deres position i trekanten og måden, de beregnes på. En trekants median er placeret inde i trekanten og beregnes ved at finde midtpunktet af en af siderne og trække en linje mellem midtpunktet og vinkelspidsen på den modsatte side. En trekants højde er placeret uden for trekanten og beregnes ved at finde den vinkelrette linje fra den modsatte vinkel til en af siderne i trekanten.
FAQs
Hvad er en trekant?
En trekant er en polygon med tre sider og tre vinkler.
Hvad er en vinkel i en trekant?
En vinkel i en trekant er et mål for, hvor meget to linjer eller sider i trekanten afviger fra at være parallelle eller vinkelret på hinanden.
Hvad er vinkelsummen i en trekant?
Vinkelsummen i en trekant er altid 180 grader. Dette betyder, at summen af de tre indre vinkler i en trekant altid vil være 180 grader.
Hvordan beregner man en trekants areal?
For at beregne en trekants areal, skal man multiplicere længden på basen med højden og dividere dette produkt med to. Formlen til at beregne et trekants areal er A = (b x h) / 2.
Hvad er Pythagoras’ sætning?
Pythagoras’ sætning er en matematisk lov, der beskriver forholdet mellem længden af de tre sider i en retvinklet trekant. Ifølge Pythagoras’ sætning er kvadratet på hypotenusen (den længste side i trekanten) lig med summen af kvadraterne på de to kateter (de to korteste sider i trekanten). Formlen for Pythagoras’ sætning er a * a + b * b = c * c, hvor a og b er længden af kateterne, og c er længden af hypotenusen.
Du kan se flere oplysninger om beregn højden i en retvinklet trekant her.
- Matematikhjælpen – Geometri – Introduktion 2. – rasmus
- Retvinklede trekanter (Matematik C, Trigonometri)
- Højde, vinkelhalveringslinje og median i en trekant – Studienet.dk
- Ligesidet trekant – MatNat.dk
- hjælp til at finde højden i en retvinklede trekant! – Matematik
- Retvinklet trekant – MatNat.dk
- Matematikhjælpen – Geometri – Introduktion 2. – rasmus
- Retvinklede trekanter – Studienet.dk
Se mere information her: https://cungcaphangchinhhang.com/danh-muc/cham-soc-da-mat-duong-the.html
så du har læst emneartiklen beregn højden i en retvinklet trekant. Hvis du fandt denne artikel nyttig, så del den med andre. Mange tak.